FUNCȚII HIPERBOLICE- Sinusul hiperbolic (sh x) și cosinusul (ch x) sunt definite de următoarele egalități:

Tangenta și cotangenta hiperbolice sunt definite prin analogie cu tangenta și cotangenta trigonometrică:

Secantele hiperbolice și cosecantele sunt definite în mod similar:

Există formule:

Proprietățile funcțiilor hiperbolice sunt în multe privințe similare cu proprietățile (vezi). Ecuațiile x=cos t, y=sin t determină cercul x²+y² = 1; ecuațiile x=сh t, y=sh t definesc hiperbola x² - y²=1. Cum funcții trigonometrice sunt determinate dintr-un cerc cu raza unitară, iar funcțiile hiperbolice sunt determinate dintr-o hiperbolă isoscelă x² - y² = 1. Argumentul t este aria dublă a triunghiului curbiliniu umbrit OME (Fig. 48), în mod similar cu faptul că pentru funcțiile circulare (trigonometrice), argumentul t este numeric egal cu dublul aria triunghiului curbiliniu OKE ( Fig. 49):

pentru cerc

pentru hiperbolă

Teoremele de adunare pentru funcțiile hiperbolice sunt similare cu teoremele de adunare pentru funcțiile trigonometrice:

Aceste analogii sunt ușor de văzut dacă variabila complexă r este luată drept argument x. Funcțiile hiperbolice sunt legate de funcțiile trigonometrice prin următoarele formule: sh x \u003d - i sin ix, ch x \u003d cos ix, unde i este unul dintre valorile rădăcinii √-1. Funcțiile hiperbolice sh x, precum și ch x: pot lua orice valori mari (de unde, desigur, unități mari), spre deosebire de funcțiile trigonometrice sin x, cos x, care pentru valori reale ​​\u200b\u200bnu poate fi mai mare de unu în valoare absolută.
Funcțiile hiperbolice joacă un rol în geometria lui Lobachevsky (vezi), sunt utilizate în studiul rezistenței materialelor, în inginerie electrică și în alte ramuri ale cunoașterii. Există, de asemenea, denumiri de funcții hiperbolice în literatură, cum ar fi sinh x; cosh x; tghx.

Poate fi scris într-o formă parametrică folosind funcții hiperbolice (așa explică numele lor).

Notăm y= b·sht , apoi x2 / a2=1+sh2t =ch2t . De unde x=± a·cht .

Astfel, ajungem la următoarele ecuații parametrice ale hiperbolei:

Y= în sht , –< t < . (6)

Orez. 1.

Semnul "+" din formula superioară (6) corespunde ramurii drepte a hiperbolei, iar semnul ""– "" corespunde ramurii din stânga (vezi Fig. 1). Vârfurile hiperbolei A(– a; 0) și B(a; 0) corespund valorii parametrului t=0.

Pentru comparație, putem da ecuațiile parametrice ale unei elipse folosind funcții trigonometrice:

X=un cost,

Y=in sint , 0 t 2p . (7)

3. În mod evident, funcția y=chx este pară și ia doar valori pozitive. Funcția y=shx este impară, deoarece :

Funcțiile y=thx și y=cthx sunt impare ca câte pentru și funcţie ciudată. Rețineți că, spre deosebire de funcțiile trigonometrice, funcțiile hiperbolice nu sunt periodice.

4. Să studiem comportamentul funcției y= cthx în vecinătatea punctului de discontinuitate x=0:

Astfel, axa y este asimptota verticală a graficului funcției y=cthx . Să definim asimptotele oblice (orizontale):

Prin urmare, linia y=1 este asimptota orizontală dreaptă a graficului funcției y=cthx . Datorită ciudățeniei acestei funcții, asimptota ei orizontală stângă este linia dreaptă y= –1. Este ușor de arătat că aceste linii sunt simultan asimptote pentru funcția y=thx. Funcțiile shx și chx nu au asimptote.

2) (chx)"=shx (afișat în mod similar).

4)

Există, de asemenea, o anumită analogie cu funcțiile trigonometrice. Masa plina derivatele tuturor funcțiilor hiperbolice sunt date în Secțiunea IV.

, pagina 6

11 Funcții de bază ale unei variabile complexe

Amintiți-vă definiția exponentului complex - . Apoi

Extinderea seriei Maclaurin. Raza de convergență a acestei serii este +∞, ceea ce înseamnă că exponentul complex este analitic pe întregul plan complex și

(exp z)"=exp z; exp 0=1. (2)

Prima egalitate de aici urmează, de exemplu, din teorema privind diferențierea termen cu termen a unei serii de puteri.

11.1 Funcții trigonometrice și hiperbolice

Sinusul unei variabile complexe numită funcție

Cosinusul unei variabile complexe exista o functie

Sinusul hiperbolic al unei variabile complexe este definit astfel:

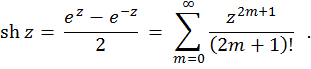
Cosinusul hiperbolic al unei variabile complexe-- este o funcție

Notăm câteva proprietăți ale funcțiilor nou introduse.

A. Dacă x∈ ℝ , atunci cos x, sin x, ch x, sh x∈ ℝ .

B. Există următoarea legătură între funcțiile trigonometrice și hiperbolice:

cos iz=ch z; sin iz=ish z, ch iz=cos z; shiz=isinz.

B. Identități trigonometrice și hiperbolice de bază:

cos2z+sin2z=1; ch2z-sh2z=1.

Dovada identității hiperbolice de bază.

Identitatea trigonometrică principală decurge din identitatea hiperbolică ononică atunci când se ia în considerare legătura dintre funcțiile trigonometrice și hiperbolice (vezi proprietatea B)

G Formule de adunare:

În special,

D. Pentru a calcula derivatele funcțiilor trigonometrice și hiperbolice, ar trebui să se aplice teorema privind diferențierea termen cu termen a unei serii de puteri. Primim:

(cos z)"=-sin z; (sin z)"=cos z; (ch z)"=sh z; (sh z)"=ch z.

E. Funcțiile cos z, ch z sunt pare, în timp ce funcțiile sin z, sh z sunt impare.

G. (periodicitate) Funcția e z este periodică cu perioada 2π i. Funcțiile cos z, sin z sunt periodice cu o perioadă de 2π, iar funcțiile ch z, sh z sunt periodice cu o perioadă de 2πi. În plus,

Aplicând formulele de sumă, obținem

Z. Descompuneri în părți reale și imaginare:

Dacă o funcție analitică cu o singură valoare f(z) mapează bijectiv un domeniu D pe un domeniu G, atunci D se numește domeniu de univalență.

ȘI. Domeniul D k ​​=( x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .

Dovada. Relația (5) implică că maparea exp:D k → ℂ este injectivă. Fie w orice număr complex diferit de zero. Apoi, rezolvând ecuațiile e x =|w| și e iy =w/|w| cu variabile reale x și y (alegem y din semiinterval); luate în considerare uneori ...... Dicţionar Enciclopedic F.A. Brockhaus și I.A. Efron

Funcții inverse față de funcțiile hiperbolice (vezi Funcții hiperbolice) sh x, ch x, th x; ele sunt exprimate prin formule (a se citi: arezin hiperbolic, cosinus suprafață hiperbolic, aretangent ... ... Marea Enciclopedie Sovietică

Funcții inverse hiperbolice. funcții; exprimat in formule... Științele naturii. Dicţionar enciclopedic

Funcțiile hiperbolice inverse sunt definite ca inversele funcțiilor hiperbolice. Aceste funcții determină aria sectorului hiperbolei unității x2 − y2 = 1 în același mod în care funcțiile trigonometrice inverse determină lungimea ... ... Wikipedia

Cărți

• Funcții hiperbolice , Yanpolsky A.R. Cartea descrie proprietățile funcțiilor hiperbolice și hiperbolice inverse și oferă relația dintre acestea și alte funcții elementare. Aplicații ale funcțiilor hiperbolice la...