Confidențialitatea dvs. este importantă pentru noi. Din acest motiv, am dezvoltat o Politică de confidențialitate care descrie modul în care folosim și stocăm informațiile dvs. Vă rugăm să citiți politica noastră de confidențialitate și anunțați-ne dacă aveți întrebări.
Colectarea și utilizarea informațiilor personale
Informațiile personale se referă la date care pot fi utilizate pentru a identifica o anumită persoană sau pentru a o contacta.
Vi se poate solicita să furnizați informațiile dvs. personale în orice moment când ne contactați.
Mai jos sunt câteva exemple de tipuri de informații personale pe care le putem colecta și cum putem folosi aceste informații.
Ce informații personale colectăm:
- Când lăsați o solicitare pe site, este posibil să colectăm diverse informații, inclusiv numele dvs., numărul de telefon, adresa de e-mail etc.
Cum folosim informațiile dvs. personale:
- Informațiile personale pe care le colectăm ne permit să vă contactăm și să raportăm despre oferte unice, promoții și alte evenimente și evenimente viitoare.
- Din când în când, putem folosi informațiile dvs. personale pentru a trimite notificări și mesaje importante.
- De asemenea, putem utiliza informații personale în scopuri interne, cum ar fi efectuarea unui audit, analiza datelor și diverse studii pentru a îmbunătăți serviciile pe care le oferim și pentru a vă oferi recomandări cu privire la serviciile noastre.
- Dacă participați la o remiză de premii, concurs sau eveniment promoțional similar, putem folosi informațiile pe care le furnizați pentru a gestiona astfel de programe.
Dezvăluirea către terți
Nu dezvăluim informațiile primite de la dvs. către terți.
excepții:
- Dacă este necesar - în conformitate cu legea, sistemul judiciar, în procedurile judiciare și / sau pe baza anchetelor publice sau a anchetelor de la organele guvernamentale din Federația Rusă - dezvăluie informațiile dvs. personale. De asemenea, putem dezvălui informații despre dvs. dacă stabilim că o asemenea divulgare este necesară sau adecvată în scopuri de securitate, menținerea legii și a ordinii sau alte cazuri importante din punct de vedere social.
- În cazul unei reorganizări, fuziuni sau vânzări, putem transfera informațiile personale pe care le colectăm către terța parte corespunzătoare, destinatarul.
Protecția informațiilor personale
Ne luăm măsuri de precauție - inclusiv cele administrative, tehnice și fizice - pentru a vă proteja informațiile personale împotriva pierderii, furtului și a utilizării neloiale, precum și de accesul, dezvăluirea, modificarea și distrugerea neautorizate.
Respectă-ți confidențialitatea la nivelul companiei
Pentru a ne asigura că informațiile dvs. personale sunt sigure, comunicăm regulile de confidențialitate și securitate angajaților noștri și monitorizăm strict implementarea măsurilor de confidențialitate.
Conceptul de poligon
Definiția 1
poligon numită figură geometrică în plan, care constă din perechi de segmente interconectate, ale căror vecine nu se află pe o linie dreaptă.
Segmentele sunt numite laturile poligonuluiși capetele lor - vârfurile poligonului.
Definiția 2
O $ n $ -gon este un poligon cu $ n $ vertexuri.
Tipuri de poligoane
Definiția 3
Dacă poligonul va sta întotdeauna pe o parte a oricărei linii care trece prin laturile sale, atunci se numește poligonul convex (fig. 1).
Figura 1. Poligonul convex
Definiția 4
Dacă un poligon se află pe laturi diferite a cel puțin unei linii drepte care trece prin laturile sale, atunci poligonul se numește non-convex (Fig. 2).

Figura 2. Poligonul neconvex
Suma unghiurilor de poligon
Introducem teorema pe suma unghiurilor unui gon.
Teorema 1
Suma unghiurilor unei -gon convexe este definită după cum urmează
\\ [(n-2) \\ cdot (180) ^ 0 \\]
Dovada.
Să ne fie dat poligonul convex $ A_1A_2A_3A_4A_5 \\ puncte A_n $. Conectați vertexul său $ A_1 $ cu toate celelalte vârfuri ale poligonului dat (Fig. 3).

Figura 3
Cu această conexiune, obținem un triunghi de $ n-2 $. Rezumând unghiurile lor obținem suma unghiurilor unui gon dat. Deoarece suma unghiurilor unui triunghi este $ (180) ^ 0, $ obținem că suma unghiurilor unui convex este determinată de formula
\\ [(n-2) \\ cdot (180) ^ 0 \\]
Teorema este dovedită.
Conceptul patrulaterului
Folosind definiția de $ 2, este ușor să introduceți definiția unui patrulater.
Definiția 5
Un patrulater este un poligon cu vârfuri de 4 $ (Fig. 4).

Figura 4. Quadrangle
Pentru un patrulater, noțiunile unui cvadrangel convex și un patrulater non-convex sunt definite în mod similar. Exemple clasice de patratele convexe sunt pătrat, dreptunghi, trapezoid, rombo, paralelogram (Fig. 5).

Figura 5. Cvadrangule convexe
Teorema 2
Suma unghiurilor unui patrulater convex este $ (360) ^ 0 $
Dovada.
Prin teorema de $ 1 $, știm că suma unghiurilor unui convex este determinată de formula
\\ [(n-2) \\ cdot (180) ^ 0 \\]
Prin urmare, suma unghiurilor unui patrulater convex este
\\ [\\ left (4-2 \\ right) \\ cdot (180) ^ 0 \u003d (360) ^ 0 \\]
Teorema este dovedită.
Definiția 1. O linie ruptă este o secvență finită de segmente, astfel încât unul dintre capetele primului segment servește ca sfârșitul celui de-al doilea, celălalt capăt al celui de-al doilea segment servește ca sfârșitul celui de-al treilea etc.
Segmentele care alcătuiesc polilinia se numesc legături. Segmentele învecinate nu se află pe o linie dreaptă. Dacă capetele poliliniei coincid, atunci se numește închis. O linie ruptă se poate încrucișa, se poate atinge și se poate sprijini pe sine. Dacă polilinia nu are astfel de caracteristici, atunci se numește simplu.
Definiția 2. O linie poligonală simplă închisă cu o parte a planului delimitat de ea se numește poligon.
Polilina în sine se numește limita poligonului, legăturile polilinii - petrecerile poligon, capetele legăturilor - vârfurile poligonului. Două laturi adiacente ale poligonului formează un unghi. Numărul de unghiuri dintr-un poligon este egal cu numărul de laturi. Fiecare poligon are unghiuri mai mici de 180 °. Lățile și colțurile poligonului sunt numite element poligon.
Un segment care leagă două vârfuri neadiacente ale unui poligon este numit diagonală. În orice n-gon, se pot desena n-2 diagonale.
Definiția 3. Se numește poligonul convexdacă se află pe o parte a fiecărei linii care conține latura ei. Poligonii care nu îndeplinesc această condiție se numesc non-convexe.
Proprietățile poligoanelor convexe.
Proprietatea 1. Un poligon convex are toate unghiurile sub 180 °.
Dovadă: Ia orice unghi A al poligonului convex P și partea sa a, pornind de la vertexul A. Fie o linie care conține latura a. Deoarece poligonul P este convex, acesta se află pe o parte a liniei l. Prin urmare, unghiul A se află pe o parte a liniei l. În consecință, unghiul A este mai mic decât unghiul desfășurat, adică РA< 180°.
Proprietatea 2. Segmentul care leagă oricare două puncte ale unui poligon convex este conținut în acest poligon.
Dovadă: luați orice două puncte M și N ale poligonului convex P. Poligonul P este intersecția mai multor jumătăți de plan. Segmentul MN se află în fiecare dintre aceste jumătăți de plan. Prin urmare, este conținut și în poligonul R.
Proprietatea 3. Suma unghiurilor unui poligon convex este (n - 2) ∙ 180 °.
Dovadă: Ia un punct arbitrar 0 în interiorul unui poligon P convex și conectează-l la toate vârfurile poligonului. Formate n triunghiuri, suma unghiurilor fiecăruia este egală cu 180 °. Unghiurile de la vârful O se ridică până la 360 ° \u003d 2 ∙ 180 °. Prin urmare, suma unghiurilor poligonului este n ∙ 180 ° - 2 ∙ 180 ° \u003d (n - 2) ∙ 180 °.
Conceptul de paralelogram. Proprietăți paralelograme.
Definiția 1. Un patrulater ale cărui laturi opuse sunt paralele sunt numite paralelogramă.
Fiecare paralelogram are patru vârfuri, patru laturi, patru unghiuri. Se numesc două părți care au capete comune înrudit. Fiecare paralelogram are două diagonale - segmente care leagă vârfurile opuse ale paralelogramului. Suma unghiurilor paralelogramei este 360 \u200b\u200b°.
Proprietăți paralelograme.
 Proprietatea 1. Într-un paralelogram, laturile opuse sunt egale, iar unghiurile opuse sunt egale în perechi.
Proprietatea 1. Într-un paralelogram, laturile opuse sunt egale, iar unghiurile opuse sunt egale în perechi.
Dovadă: desenează un difuzor în diagonală. AC - general;
ÐВАС \u003d ÐАСD (cruce internă situată la AB II î.Hr. și sec. AC);
ÐВСА \u003d ÐСАД (cruce interioară situată la AD II î.Hr. și sec. AC);
Þ DABC \u003d DADC (după 2 criterii).
AB \u003d CD; BC \u003d AD; LB \u003d ld.
ÐА \u003d ÐВАС + ÐСAD; ÐÐ \u003d ÐАСB + ÐАСD; Þ ÐА \u003d ÐС.
Proprietatea 2. Într-un paralelogram, unghiurile adiacente unei părți se adaugă până la 180 °.
dovada:
РВ + РА \u003d 180 ° (intern unilateral la BC II AD și secant AB).
ÐB + ÐÐ \u003d 180 ° (intern pe o parte cu AB II CD și secant BC).
ÐD + ÐC \u003d 180 ° (intern unilateral cu BC II AD și CD secantant).
ÐA + ÐD \u003d 180 ° (internă pe o parte cu AB II CD și AD secant).
Proprietatea 3. Diagonalele unui paralelogram sunt împărțite la jumătate de punctul de intersecție.
 Dovadă: Desenăm diagonalele AC și BD care se intersectează în punctul O.
Dovadă: Desenăm diagonalele AC și BD care se intersectează în punctul O.
AB \u003d CD (conform primului paralelogram St.-w);
ÐAВO \u003d ÐODC (cruce internă situată la AB II CD și secantă BD);
ÐBAO \u003d ÐOСD (cruce internă situată la AB II CD și AC secant);
Þ DAVO \u003d DODС (după 2 criterii).
BO \u003d OD; AO \u003d OC.
Semne ale unui paralelogram.
Semnul 1. Dacă două laturi sunt egale și paralele într-un patrulater, atunci acest patrulater este o paralelogramă.
 Date: ABCD - un patrulater; AD II î.Hr.,
Date: ABCD - un patrulater; AD II î.Hr.,
Conceptul de poligon
Definiția 1
poligon numită figură geometrică în plan, care constă din perechi de segmente interconectate, ale căror vecine nu se află pe o linie dreaptă.
Segmentele sunt numite laturile poligonuluiși capetele lor - vârfurile poligonului.
Definiția 2
O $ n $ -gon este un poligon cu $ n $ vertexuri.
Tipuri de poligoane
Definiția 3
Dacă poligonul va sta întotdeauna pe o parte a oricărei linii care trece prin laturile sale, atunci se numește poligonul convex (fig. 1).
Figura 1. Poligonul convex
Definiția 4
Dacă un poligon se află pe laturi diferite a cel puțin unei linii drepte care trece prin laturile sale, atunci poligonul se numește non-convex (Fig. 2).

Figura 2. Poligonul neconvex
Suma unghiurilor de poligon
Introducem teorema pe suma unghiurilor unui gon.
Teorema 1
Suma unghiurilor unei -gon convexe este definită după cum urmează
\\ [(n-2) \\ cdot (180) ^ 0 \\]
Dovada.
Să ne fie dat poligonul convex $ A_1A_2A_3A_4A_5 \\ puncte A_n $. Conectați vertexul său $ A_1 $ cu toate celelalte vârfuri ale poligonului dat (Fig. 3).

Figura 3
Cu această conexiune, obținem un triunghi de $ n-2 $. Rezumând unghiurile lor obținem suma unghiurilor unui gon dat. Deoarece suma unghiurilor unui triunghi este $ (180) ^ 0, $ obținem că suma unghiurilor unui convex este determinată de formula
\\ [(n-2) \\ cdot (180) ^ 0 \\]
Teorema este dovedită.
Conceptul patrulaterului
Folosind definiția de $ 2, este ușor să introduceți definiția unui patrulater.
Definiția 5
Un patrulater este un poligon cu vârfuri de 4 $ (Fig. 4).

Figura 4. Quadrangle
Pentru un patrulater, noțiunile unui cvadrangel convex și un patrulater non-convex sunt definite în mod similar. Exemple clasice de patratele convexe sunt pătrat, dreptunghi, trapezoid, rombo, paralelogram (Fig. 5).

Figura 5. Cvadrangule convexe
Teorema 2
Suma unghiurilor unui patrulater convex este $ (360) ^ 0 $
Dovada.
Prin teorema de $ 1 $, știm că suma unghiurilor unui convex este determinată de formula
\\ [(n-2) \\ cdot (180) ^ 0 \\]
Prin urmare, suma unghiurilor unui patrulater convex este
\\ [\\ left (4-2 \\ right) \\ cdot (180) ^ 0 \u003d (360) ^ 0 \\]
Teorema este dovedită.
Set de puncte convexe din avion.
Multe puncte de pe un plan sau într-un spațiu tridimensional sunt numite convexdacă două puncte ale acestui set pot fi conectate de un segment de linie care se află complet în acest set.
Teorema 1. Intersecția unui număr finit de seturi convexe este un set convex.
Corolar. Intersecția unui număr finit de seturi convexe este un set convex.
Punctele de colț.
Punctul de delimitare al unui set convex se numește unghiulardacă este posibil să tragem un segment prin el, toate punctele care nu aparțin acestui set.
Seturile diferite de forme pot avea un număr finit sau infinit de puncte de colț.
Poligonul convex.
poligon Se numește convexdacă se întinde pe o parte a fiecărei linii care trece prin cele două vârfuri ale sale învecinate.
Teorema: Suma unghiurilor unui n-gon convex este 180˚ * (n-2)
6) Soluția sistemelor de inegalități m liniare cu două variabile
Este dat un sistem de m inegalități liniare cu două variabile
Semnele unor inegalități sau ale tuturor inegalităților pot fi ≥.
Luați în considerare prima inegalitate în sistemul de coordonate X1OX2. Construiți o linie dreaptă
care este linia de delimitare.
Această linie dreaptă împarte planul în două jumătăți plane 1 și 2 (Fig. 19.4).
Semiplanul 1 conține originea, jumătatea planului 2 nu conține originea.
Pentru a determina ce parte a liniei de delimitare se află jumătatea plană dată, trebuie să luăm un punct arbitrar pe plan (originea este mai bună) și să inlocuim coordonatele acestui punct în inegalitate. Dacă inegalitatea este adevărată, atunci jumătatea planului este întoarsă spre acest punct, dacă nu chiar corectă, atunci în direcția opusă din punctul respectiv.
Direcția semiclanului din figuri este arătată de săgeată.
Definiția 15. Soluția la fiecare inegalitate din sistem este un semiplanșă care conține o linie de delimitare și situată pe o parte a acestuia.
Definiția 16. Intersecția semiclanurilor, fiecare dintre acestea fiind determinată de inegalitatea corespunzătoare a sistemului, este denumită domeniul soluției sistemului (RR).
Definiția 17. Domeniul unei soluții la un sistem care îndeplinește condițiile de non-negativitate (xj ≥ 0, j \u003d) este denumit domeniul soluțiilor (negativ) sau neadmisibile (ODR).
Dacă sistemul de inegalități este compatibil, atunci OR și ODR pot fi un poliedru, o regiune poliedrică nelimitată sau un singur punct.
Dacă sistemul de inegalități este incompatibil, atunci OR și ODD sunt un set gol.
Exemplul 1. Găsiți inegalitățile sistemului OD și ODR și determinați coordonatele punctelor de colț ale ODR
Decizie. Găsim OR-ul primei inegalități: x1 + 3x2 ≥ 3. Construim linia de graniță x1 + 3x2 - 3 \u003d 0 (Fig. 19.5). Înlocuim coordonatele punctului (0,0) în inegalitate: 1 ∙ 0 + 3 ∙ 0\u003e 3; întrucât coordonatele punctului (0,0) nu-l satisfac, soluția inegalității (19.1) este un semiplan care nu conține punctul (0,0).
În mod similar, găsim soluții pentru inegalitățile rămase ale sistemului. Constatăm că OD și ODD ale sistemului de inegalități este un ABCD poliedru convex.
Găsiți punctele de colț ale poliedrului. Punctul A este definit ca punctul de intersecție a liniilor
Rezolvând sistemul, obținem A (3/7, 6/7).
Găsiți punctul B ca punct de intersecție a liniilor
Din sistem obținem B (5/3, 10/3). În mod similar, găsim coordonatele punctelor C și D: C (11/4; 9/14), D (3/10; 21/10).
Exemplul 2. Găsiți inegalitățile sistemului OR și ODR
Decizie. Construim linii și definim soluții pentru inegalități (19.5) - (19.7). OR și ODR sunt zone poliedrice nelimitate ale ACFM și respectiv ABDEKM (Fig. 19.6).
Exemplul 3. Găsiți inegalitățile sistemului OR și ODR
Decizie. Găsim soluții la inegalități (19.8) - (19.10) (Fig. 19.7). Programul operațional reprezintă o regiune ABC multifacetă nelimitată; ODR - punctul B.
Exemplul 4. Găsiți inegalitățile sistemului OP și ODR
Decizie. Construind liniile, găsim soluții la inegalitățile sistemului. RR și ODR sunt incompatibile (Fig. 19.8).
EXERCITII
Găsiți sisteme de inegalități OR și ODR
Teorema. Dacă xn ® a, atunci.
Dovada. Din xn ® a rezultă că. În același timp:
Ie , adică . Teorema este dovedită.
Teorema. Dacă xn ® a, atunci secvența (xn) este delimitată.
Trebuie menționat că inversul nu este adevărat, adică delimitarea unei secvențe nu implică convergența acesteia.
De exemplu, secvența nu are limită, deși
Extinderea funcțiilor în seria de putere.
Extinderea funcțiilor dintr-o serie de putere are o importanță deosebită pentru rezolvarea diverselor probleme de studiere a funcțiilor, diferențierea, integrarea, rezolvarea ecuațiilor diferențiale, calcularea limitelor și calcularea valorilor aproximative ale unei funcții.
Total obținem:
Luați în considerare o metodă de extindere a unei funcții într-o serie folosind integrarea.
Cu ajutorul integrării, este posibil să se extindă într-o serie o astfel de funcție pentru care se cunoaște sau se poate găsi cu ușurință expansiunea într-o serie a derivatului său.
Găsim diferențialul funcției și o integrăm în intervalul de la 0 la x.

 Pro și contra contra educației sovietice
Pro și contra contra educației sovietice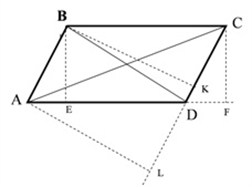 Paralelogramă și proprietățile sale
Paralelogramă și proprietățile sale Probleme de mediu la nivel global
Probleme de mediu la nivel global