Definiția. O figură delimitată de un grafic al unei funcții continue, constant-semn f (x), axa abscisă și linii drepte x \u003d a, x \u003d b, se numește trapez curbat.

Moduri de a găsi zona unui trapez curbat

Teorema. Dacă f (x) este o funcție continuă și non-negativă pe un segment, atunci aria trapezului curbat corespunzător este egală cu incrementul antiderivatelor.

Date: f (x) - neopr continuu. funcție, xO.

Dovedește: S \u003d F (b) - F (a), unde F (x) este antiderivativul lui f (x).

dovada:

1) Luați în considerare funcția auxiliară S (x). La fiecare xО se asociază acea parte a trapezului curb care se află în stânga liniei drepte (Fig. 2) care trece printr-un punct cu această abscisă și paralelă cu axa ordonată.

Prin urmare, S (a) \u003d 0 și S (b) \u003d S

Să demonstrăm că S (a) este antiderivativul lui f (x).

D (f) \u003d D (S) \u003d

S "(x0) \u003d lim (S (x0 + Dx) - S (x0) / Dx), pentru Dx®0 DS - dreptunghi

Dx®0 cu laturile Dx și f (x0)

S "(x0) \u003d lim (Dx f (x0) / Dx) \u003d lim f (x0) \u003d f (x0): deoarece x0 este un punct, atunci S (x) -

Dx®0 Dx®0 antiderivativ f (x).

Prin urmare, prin teorema formei generale, antiderivativul S (x) \u003d F (x) + C.

pentru că S (a) \u003d 0, apoi S (a) \u003d F (a) + C

S \u003d S (b) \u003d F (b) + C \u003d F (b) -F (a)

1). Împărțiți segmentul în n părți egale. Etapa de despărțire (Fig. 3)

Dx \u003d (b-a) / n. Mai mult, Stp \u003d lim (f (x0) Dx + f (x1) Dx + ... + f (xn)) Dx \u003d n®Ґ \u003d lim Dx (f (x0) + f (x1) + ... + f (xn))

Pentru n®Ґ obținem că Sрр \u003d Dx (f (x0) + f (x1) + ... + f (xn))

Limita acestei sume este numită integrală definitivă.

Suma sub limita se numeste suma integrala.

O integrală definită este limita sumei integrale pe un segment ca n®Ґ. Suma integrală este obținută ca limită a sumei produselor din lungimea segmentului obținută prin împărțirea domeniului de definire a funcției în orice punct al acestui interval.

a este limita inferioară a integrării;

b este partea de sus.

Formula Newton-Leibniz.

Comparând formele de zonă ale unui trapez curbat, concluzionăm:

dacă F este primitiv pentru b on, atunci

m f (x) dx \u003d F (b) -F (a)

m f (x) dx \u003d F (x) φ \u003d F (b) - F (a)

Proprietățile unei integrale definite.

t f (x) dx \u003d t f (z) dz

t f (x) dx \u003d F (a) - F (a) \u003d 0

t f (x) dx \u003d - t f (x) dx

f (x) dx \u003d F (a) - F (b) t f (x) dx \u003d F (b) - F (a) \u003d - (F (a) - F (b))

Dacă a, b și c sunt orice puncte ale intervalului I pe care funcția continuă f (x) are o primitivă, atunci

t f (x) dx \u003d t f (x) dx + t f (x) dx

F (b) - F (a) \u003d F (c) - F (a) + F (b) - F (c) \u003d F (b) - F (a)

(aceasta este proprietatea aditivității unei anumite integrale)

Dacă l și m suntem constanți, atunci

t (lf (x) + m j (x)) dx \u003d l t f (x) dx + m tj (x)) dx -

Aceasta este proprietatea liniarității unei integrale definite.

t (f (x) + g (x) + ... + h (x)) dx \u003d t f (x) dx + t g (x) dx + ... + t h (x) dx

m (f (x) + g (x) + ... + h (x)) dx \u003d (F (b) + G (b) + ... + H (b)) - (F (a) + G (a) + ... + H (a)) + C \u003d F (b) -F (a) + C1 + G (b) -G (a) + C2 + ... + H (b) -H (a) + Cn \u003d bbb \u003d t f (x) dx + t g (x) dx + ... + t h (x) dx

Un set de imagini standard (Fig. 4, 5, 6, 7, 8)

Fig. 4

Fig. 6 Fig. 7

pentru că f (x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0.

Este necesar: să se ia în considerare simetria funcției în raport cu axa OX. ABCD®A "B" CD b

S (ABCD) \u003d S (A "B" CD) \u003d t -f (x) dx

S \u003d t f (x) dx \u003d t g (x) dx

S \u003d t (f (x) -g (x)) dx + t (g (x) -f (x)) dx

S \u003d m (f (x) + m-g (x) -m) dx \u003d

m (f (x) - g (x)) dx

t ((f (x) -g (x)) dx

S \u003d m (f (x) + m-g (x) -m) dx \u003d

T (f (x) - g (x)) dx

Dacă pe intervalul f (x) іg (x), atunci zona dintre aceste grafice este

t ((f (x) -g (x)) dx

Funcțiile f (x) și g (x) sunt arbitrare și non-negative

S \u003d t f (x) dx - t g (x) dx \u003d t (f (x) -g (x)) dx

  Definiția.   Diferența F (b) - F (a) se numește integrală a funcției f (x) pe intervalul [a; b] și se notează după cum urmează: \u003d F (b) - F (a) este formula Newton-Leibniz.

  Sensul geometric al integralei.

Zona trapezului curbat, limitată de graficul pozitivului continuu în decalajul [a; b] funcțiile f (x), axa Ox și liniile drepte x \u003d a și x \u003d b:

  Calcularea suprafețelor folosind integrală.

1. Zona figurii, limitată de un grafic negativ continuu pe decalajul [a; b] funcțiile f (x), axa Ox și liniile drepte x \u003d a și x \u003d b:

2. Zona figurii delimitate de graficele funcțiilor continue f (x) și de liniile drepte x \u003d a, x \u003d b:

3. Zona figurii delimitate de graficele funcțiilor continue f (x) și:

4. Zona figurii delimitate de graficele funcțiilor continue f (x) și axa Ox:

Sarcini și teste pe tema "Integral. Calcularea zonelor care utilizează integralul"

• integrală

  Lecții: 4 Sarcini: 13 Teste: 1

• Calcularea suprafețelor cu integrale   - clasa 11 primitivă și integrală

  Lecții: 1 Sarcini: 10 Teste: 1

• antiderivative   - clasa 11 primitivă și integrală

  Lecții: 1 Sarcini: 11 Teste: 1

• Planimetrie: calcularea lungimilor și a suprafețelor

  Sarcini: 7

• Calcule și conversii   - Pregătirea examenului la examenul de matematică la matematică

  Sarcini: 10

Înainte de a începe să calculați aria unei cifre delimitate de linii date, încercați să desenați această figură într-un sistem de coordonate. Acest lucru va facilita foarte mult soluția problemei.

Studierea materialelor teoretice pe acest subiect vă oferă posibilitatea de a stăpâni conceptele de antiderivativ și integral, de a învăța conexiunea dintre ele, de a stăpâni cea mai simplă tehnică de calcul integral, de a învăța cum să aplicați integralul pentru a calcula aria cifrelor delimitate de graficele funcționale.

Exemple.

1. Calculați integralul

soluţie:

Răspunsul este: 0.

2. Găsiți zona figurii delimitate de linii

a)   f(   x) = 2   x –   x   2 și abscisa

soluţie:   Graficul funcției f (x) \u003d 2x - x 2 parabola. Sus: (1; 1).

Răspunsul este:(unități pătrate).

Integral categoric. Cum se calculează aria unei cifre

Ne orientăm la considerarea aplicațiilor de calcul integral. În această lecție vom analiza problema tipică și cea mai frecventă. - cum se calculează aria unei figuri plane folosind o anumită integrală. În cele din urmă, căutătorii de sens în matematica superioară - pot găsi. Nu știi niciodată. În viață, va trebui să aproximați zona cabanei cu funcții elementare și să găsiți zona folosind o anumită integrală.

Pentru dezvoltarea cu succes a materialului, este necesar:

1) Înțelegeți integrala nedeterminată cel puțin la un nivel mediu. Astfel, manechinele ar trebui să se familiarizeze mai întâi cu lecția. nu.

2) Fiți capabili să aplicați formula Newton-Leibniz și să calculați o anumită integrală. Puteți stabili prietenii calde cu anumite integrale pe pagină Integral categoric. Exemple de soluție.

De fapt, pentru a găsi aria unei figuri, nu este nevoie de atâtea cunoștințe pe o integrală nedeterminată și definită. Sarcina „calculează aria folosind o anumită integrală” implică întotdeauna construirea unui desenPrin urmare, cunoștințele și abilitățile dvs. în desenele de construcții vor fi o problemă mult mai relevantă. În acest sens, este util să reîmprospătați memoria graficelor funcțiilor elementare de bază și, cel puțin, să puteți construi o linie dreaptă, parabola și hiperbola. Acest lucru poate fi realizat (mulți au nevoie) folosind material metodologic și un articol despre transformările geometrice ale graficelor.

De fapt, toată lumea este familiarizată cu sarcina de a găsi zona folosind o anumită integrală încă de la școală și vom merge puțin înainte de programa școlară. Este posibil ca acest articol să nu se fi întâmplat deloc, dar faptul este că problema este întâlnită în 99 de cazuri din 100, când un student este chinuit de un turn urât, cu entuziasmul care stăpânește un curs de matematică superioară.

Materialele acestui atelier sunt prezentate simplu, în detaliu și cu un minim de teorie.

Să începem cu un trapez curbat.

Trapez curbat se numește o figură plană delimitată de o axă, linii drepte și un grafic al unei funcții continue pe un segment care nu schimbă semnul pe acest interval. Să fie localizată această cifră nu mai jos   axa abscisă:

atunci aria unui trapez curbat este egal numeric cu o anumită integrală. Orice integrală specifică (care există) are un sens geometric foarte bun. În lecție Integral categoric. Exemple de soluție   Am spus că o integrală certă este un număr. Și acum este timpul să precizăm un alt fapt util. Din punct de vedere al geometriei, o integrală certă este AREA.

Adică o anumită integrală (dacă există) corespunde geometric cu aria unei anumite figuri. De exemplu, ia în considerare o anumită integrală. Integrandul definește un plan pe planul de deasupra axei (cei care doresc pot trasa), iar integralul definit este egal numeric cu aria trapezului curb corespunzător.

Exemplul 1

Aceasta este o declarație de muncă tipică. Primul și cel mai important punct al soluției este construcția desenului. Mai mult, desenul trebuie construit DREAPTA.

Când construiți un desen, vă recomand următoarea comandă: la început   este mai bine să construiți toate liniile (dacă există) și numai atunci   - parabolele, hiperbolele, graficele altor funcții. Graficele funcționale sunt mai profitabile de construit pointwise, tehnica construcției punctuale poate fi găsită în materialul de referință Graficele și proprietățile funcțiilor elementare. Acolo puteți găsi materiale foarte utile pentru lecția noastră - cum să construiți rapid o parabolă.

În această problemă, soluția poate arăta astfel.
   Să executăm desenul (rețineți că ecuația definește axa):

   Nu voi ecloza trapezul curvilin, este evident aici despre ce fel de zonă vorbim. Soluția continuă astfel:

Pe segment se află graficul funcțional peste axa, prin urmare:

Răspunsul este:

Cine are dificultăți în a calcula o anumită integrală și a aplica formula Newton-Leibniz referiți la prelegere Integral categoric. Exemple de soluție.

După finalizarea sarcinii, este întotdeauna util să ne uităm la desen și să ne dăm seama dacă răspunsul a fost real. În acest caz, „prin ochi” numărăm celulele din desen - ei bine, aproximativ 9 vor fi tastați, se pare că este adevărat. Este perfect clar că dacă am avea, să spunem, un răspuns: 20 de unități pătrate, atunci este evident că a fost făcută o greșeală undeva - în mod evident, 20 de celule nu se pot încadra în figura în cauză, există zeci de forțe. Dacă răspunsul este nu, atunci sarcina este, de asemenea, rezolvată incorect.

Exemplul 2

Calculați aria figurii delimitate de liniile ,, și axa

Acesta este un exemplu pentru o soluție independentă. Soluție completă și răspuns la sfârșitul lecției.

Ce trebuie să faceți dacă este localizat un trapez curbat sub axa?

Exemplul 3

Calculați aria figurii delimitate de linii și axe de coordonate.

decizie: Să executăm desenul:

   Dacă este localizat trapezul curbat   sub axă   (sau cel puțin nu mai mare   axă dată), atunci zona sa poate fi găsită după formula:
   În acest caz:

Atenție! Două tipuri de sarcini nu trebuie confundate.:

1) Dacă vi se cere să rezolvați o anumită integrală fără niciun sens geometric, atunci poate fi negativ.

2) Dacă vi se cere să găsiți zona figurii folosind o anumită integrală, atunci zona este întotdeauna pozitivă! De aceea, minusul apare doar în formula tocmai luată în considerare.

În practică, cel mai adesea figura este situată în planurile superioare și inferioare și, prin urmare, din cele mai simple sarcini școlare, apelăm la exemple mai semnificative.

Exemplul 4

Găsiți zona unei figuri de plan delimitate de linii ,.

decizie: Mai întâi trebuie să completați desenul. În general, atunci când construim un desen pentru probleme de zonă, ne interesează cel mai mult punctele de intersecție a liniilor. Găsiți punctele de intersecție ale parabolei și ale liniei. Există două modalități de a face acest lucru. Prima metodă este analitică. Rezolvăm ecuația:

Prin urmare, limita inferioară a integrării, limita superioară a integrării.
Dacă este posibil, cel mai bine este să nu utilizați această metodă..

Este mult mai profitabil și mai rapid să construiți linii în sens, în timp ce limitele integrării sunt clarificate ca și de unul singur. Tehnica construcției punctuale pentru diferite grafice este discutată în detaliu în ajutor Graficele și proprietățile funcțiilor elementare   . Cu toate acestea, metoda analitică de a găsi limitele trebuie încă uneori folosită dacă, de exemplu, graficul este suficient de mare, sau construcția simplificată nu dezvăluie limitele de integrare (ele pot fi fracționale sau iraționale). Și un astfel de exemplu, vom lua în considerare și.

Revenim la sarcina noastră: este mai rațional să construim mai întâi o linie dreaptă și abia apoi o parabolă. Să executăm desenul:

   Repet că în construcția punct cu punct, limitele integrării sunt de cele mai multe ori clarificate „automat”.

Și acum formula de lucru: Dacă pe un segment o anumită funcție continuă mai mare sau egal   unele funcții continue, apoi aria figurii delimitate de graficele acestor funcții și linii drepte, poate fi găsită prin formula:

Aici nu trebuie să vă gândiți unde se află figura - deasupra axei sau sub axă și, mai degrabă, este important ce program este DESPRE(în raport cu un alt grafic) și care dintre ele este ACUM.

În exemplul considerat, este evident că pe segmentul parabola este situat deasupra liniei și, prin urmare, este necesar să scădem din

Completarea soluției poate arăta astfel:

Figura dorită este delimitată de o parabolă de sus și de o linie de jos.
   Pe segment, conform formulei corespunzătoare:

Răspunsul este:

De fapt, formula școlară pentru zona unui trapez curbat în jumătatea planului inferior (a se vedea exemplul simplu nr. 3) este un caz special al formulei . Deoarece axa este dată de ecuație, iar graficul funcției este localizat nu mai mare   axa atunci

Și acum câteva exemple pentru o soluție independentă

Exemplul 5

Exemplul 6

Găsiți zona figurii delimitate de linii,.

În rezolvarea problemelor de calcul al zonei folosind o anumită integrală, uneori se întâmplă un incident amuzant. Desenul este corect, calculele sunt corecte, dar prin neglijență ... zona cifrei greșite a fost găsită, așa este umilul tău servitor încurcat de mai multe ori. Iată un caz real din viață:

Exemplul 7

Calculați aria figurii delimitate cu linii ,,,.

decizie: Mai întâi, executați desenul:

... Eh, desenul rahat a ieșit, dar totul pare a fi lizibil.

Figura a cărei zonă trebuie să o găsim este umbrită în albastru.   (priviți cu atenție starea - care este limitarea figurii!). Dar, în practică, din neatenție, apare adesea un „glitch” care trebuie să găsești zona figurii, care este umbrită în verde!

Acest exemplu este util și prin faptul că, în el, zona figurii este calculată folosind două integrale definite. într-adevăr:

1) O linie este reprezentată pe o linie deasupra axei;

2) Pe segmentul de deasupra axei se află un grafic al hiperbolei.

Este evident că pătratele pot fi (și ar trebui) aplatizate, prin urmare:

Răspunsul este:

Trecem la o sarcină mai substanțială.

Exemplul 8

Calculați aria cifrei delimitate de linii,
   Vom prezenta ecuațiile sub forma „școlii” și vom efectua un desen punct cu punct:

   Din desen se poate observa că limita noastră superioară este „bună”:.
   Dar care este limita inferioară ?! Este clar că acesta nu este un număr întreg, dar care? Poate? Dar unde este garanția că desenul este făcut cu o acuratețe perfectă, se poate foarte bine. Sau rădăcina. Și dacă nu am făcut programul corect?

În astfel de cazuri, trebuie să petreceți timp suplimentar și să rafinați limitele integrării în mod analitic.

Găsiți punctele de intersecție ale liniei și parabolei.
   Pentru a face acest lucru, rezolvăm ecuația:


,

Într-adevăr ,.

Soluția suplimentară este banală, principalul lucru nu este să vă confundați cu permutările și semnele, aici calculele nu sunt cele mai ușoare.

Pe segment conform formulei corespunzătoare:

Răspunsul este:

Ei bine, și în încheierea lecției, vom considera două sarcini mai dificile.

Exemplul 9

Calculați aria figurii delimitate cu linii ,,

decizie: Să desenăm această figură în desen.

La naiba, am uitat să semnez programul și să refac poza, îmi pare rău, nu un hotman. Nu un desen, pe scurt, astăzi este ziua \u003d)

Pentru construcția fără sens, este necesar să cunoaștem aspectul sinusoidului (și, în general, este util să cunoaștem grafice ale tuturor funcțiilor elementare), precum și unele valori ale sinusului, pot fi găsite în tabel trigonometric. Într-o serie de cazuri (ca în acest caz), este permis să se construiască un desen schematic, pe care grafiile și limitele de integrare trebuie să fie afișate corect în principiu.

Nu există probleme cu limitele de integrare, ele urmează direct de la condiția: - „X” se schimbă de la zero la „pi”. Redactăm o altă soluție:

Pe segment, graficul funcțional este situat deasupra axei, prin urmare:

Luați în considerare un trapezoid curbat delimitat de axa Ox, curba y \u003d f (x) și două linii drepte: x \u003d a și x \u003d b (Fig. 85). Luăm o valoare arbitrară a lui x (nu numai a și nu b). Îi dăm un increment h \u003d dx și considerăm o bandă delimitată prin drepte AB și CD, axa Ox și arcul BD aparținând curbei luate în considerare. Vom numi această bandă o fâșie elementară. Zona benzii elementare diferă de aria dreptunghiului ACQB de triunghiul curbat BQD, iar aria acesteia din urmă este mai mică decât aria dreptunghiului BQDM cu laturile BQ \u003d h \u003d dx) QD \u003d Ay și o suprafață egală cu hAy \u003d Ay dx. Odată cu scăderea laturii h, latura Du scade de asemenea și simultan cu h tinde spre zero. Prin urmare, aria BQDM este infinitesimală de ordinul doi. Zona benzii elementare este creșterea zonei, iar aria dreptunghiului ACQB, egală cu AB-AC \u003d\u003d / (x) dx\u003e este diferența de zonă. Prin urmare, găsim zona însăși prin integrarea diferențialului său. În cadrul figurii analizate, variabila independentă n: variază de la a la b, astfel încât zona dorită 5 va fi egală cu 5 \u003d \\ f (x) dx. (I) Exemplul 1. Calculăm aria delimitată de parabola y - 1-x *, dreptele X \u003d -Fj-, x \u003d 1 și axa O * (Fig. 86). în Fig. 87. Fig. 86. 1 Aici f (x) \u003d 1 -??, Limitele de integrare sunt a \u003d - și \u003d \u003d 1, prin urmare J [* -m] \\ - -fl - -1 -1- ± __1V1 -ll-I- ^ 3) | _ 2 3V 2 / J 3 24 24 * Exemplu 2. Calculăm aria delimitată de axa sinusoidă y \u003d sinXy Ox și de linia dreaptă (Fig. 87). Folosind formula (I), obținem Л 2 S \u003d J sinxdx \u003d [-cos x] Q \u003d 0 - (- 1) \u003d lf Exemplul 3. Calculăm aria delimitată de arcul sinusoidului ^ y \u003d sin jc închis între două puncte de intersecție adiacente. cu axa Ox (de exemplu, între origine și punctul cu abscisa I). Rețineți că, din considerente geometrice, este clar că această zonă va fi de două ori mai mare decât cea a exemplului precedent. Cu toate acestea, vom face calculele: I 5 \u003d | s \\ nxdx \u003d [- cosx) * - - cos i - (- cos 0) \u003d 1 + 1 \u003d 2. о Într-adevăr, presupunerea noastră s-a dovedit a fi valabilă. Exemplul 4. Calculați zona delimitată de sinusoid și de axa ^ Ox într-o singură perioadă (Fig. 88). Analiza preliminară a hotărârilor sugerează că suprafața va fi de patru ori mai mare decât în \u200b\u200bproiectul 2. Cu toate acestea, după efectuarea calculelor, obținem „i Г, * i S - \\ sin x dx \u003d [- cos x] 0 \u003d - - cos 2l - (- cos 0) \u003d - 1 + 1 \u003d 0. Acest rezultat necesită clarificări. Pentru a clarifica esența materiei, de asemenea, calculăm aria delimitată de același sinusoid y \u003d sin l: și axa Ox în intervalul de la l la 2π. Folosind formula (I), obținem 2l $ 2l sin xdx \u003d [- cosx] l \u003d -cos 2π ~) -c05ya \u003d - 1-1 \u003d -2. Astfel, vedem că această zonă s-a dovedit a fi negativă. Comparând-o cu aria calculată în pr. 3, descoperim că valorile lor absolute sunt aceleași, iar semnele sunt diferite. Dacă aplicăm proprietatea V (vezi Ch. XI, § 4), atunci obținem 2l și 2l J sin xdx \u003d J sin * dx [sin x dx \u003d 2 + (- 2) \u003d 0 din întâmplare. Întotdeauna zona de sub axa Ox, cu condiția ca variabila independentă să se schimbe de la stânga la dreapta, se obține calculând negativul prin integrale. În acest curs, vom avea întotdeauna în vedere zone fără semne. Prin urmare, răspunsul din exemplul examinat va fi acesta: zona dorită este 2 + | -2 | \u003d 4. Exemplul 5. Să calculăm aria OAB indicată în Fig. 89. Această zonă este delimitată de axa Ox, parabola y \u003d - xr și de linia dreaptă y - \u003d -x + 1. Zona trapezului curbat Zona căutată a OAB este formată din două părți: OAM și MAV. Deoarece punctul A este punctul de intersecție al parabolei și linia dreaptă, găsim coordonatele sale rezolvând sistemul de ecuații 3 2 Y \u003d mx. (trebuie să găsim doar abscisa punctului A). Rezolvând sistemul, găsim l; \u003d ~. Prin urmare, suprafața trebuie calculată în părți, mai întâi pl. OAM, și apoi pl. MAV: .... Г 3 2, 3 Г х П 3 1/2 У 2. QAM- ^ x și let F (x)   - unele dintre primitive. Apoi numărul F (b) –F (a)   numită integrală a și   la b   funcțiile f (x)   și este desemnat

.

egalitate
  se numește formula Newton - Leibniz.

Această formulă conectează problema găsirii zonei unei figuri plane cu o integrală.

În general, dacă o cifră este limitată de graficele funcționale y \u003d f (x);   y \u003d g (x) (f (x)\u003e g (x)) și direct x \u003d a;   x \u003d batunci suprafața sa este egală cu:

.

Exemplul 2.   În ce punct al graficului funcțional y \u003d x 2 + 1 este necesar să tragem o tangentă astfel încât să taie figura formată de graficul acestei funcții și de linii drepte y \u003d0, x \u003d0, x \u003d1 trapez din cea mai mare zonă?

Decizie.   lăsa M 0 (x 0 , da 0 )   - punctul grafic al funcției y \u003d x 2 + 1, în care este desenată tangenta dorită.

Găsiți ecuația tangentă y \u003d y 0 + f (x 0 ) (x - x 0 ) .

Avem:

prin urmare

.

Găsiți zona trapezului OABC.

.

B   - punctul de intersecție a tangentei cu linia x \u003d1 

Problema a fost redusă la găsirea celei mai mari valori a funcției

S(x)\u003d –X 2 + x +1 pe segment. Va găsi S (x)=– 2x +1. Găsiți punctul critic din afecțiune S (x)= 0  x \u003d.

Vedem că funcția atinge valoarea maximă când x \u003d. Va găsi
.

Răspunsul este:   tangenta trebuie trasă la
.

Rețineți că problema găsirii integralei este adesea întâlnită pe baza semnificației sale geometrice. Să arătăm prin exemplu cum se rezolvă o astfel de problemă.

Exemplul 4   Folosind sensul geometric al integralei pentru a calcula

și )
; b)
.

Decizie.

a)
- egală cu aria trapezului curbat, limitată de linii.

P ne transformăm

  - jumătatea superioară a cercului centrat P(1; 0) și raza R \u003d1.

prin urmare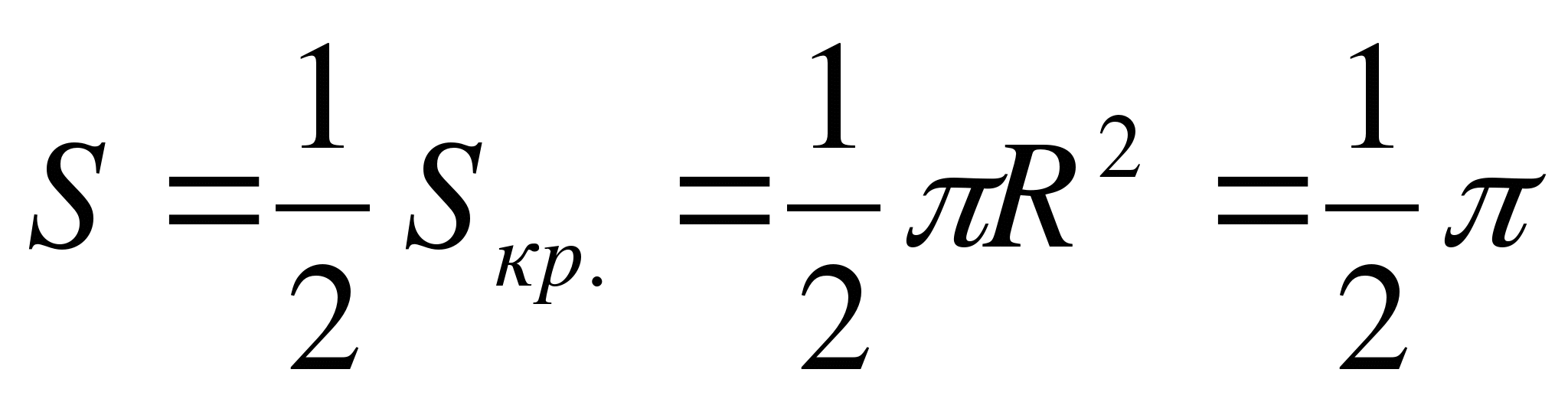
.

Răspunsul este:
.

b) Arătând într-un mod similar, construim o regiune delimitată de grafice – 2x +2, tangent cu acesta în puncte A
, B(4;2)

y \u003d–9x-59, parabola y \u003d3x 2 + topor +1, dacă se știe că tangenta la o parabolă la x \u003d -2 alcătuiește cu axa bou unghiul de mărime arctg6.

A găsi șidacă se știe că zona unui trapez curbat delimitat de linii y \u003d3x 3 + 2x, x \u003d a, y \u003d0 este egal cu unul.

Găsiți cea mai mică valoare a zonei unei figuri delimitate de o parabolă y \u003d x 2 + 2x-3 și direct   y \u003d kx +1.

6. Informații privind temele pentru acasă.

Sarcini: Pentru a le oferi elevilor o înțelegere a scopului, conținutului și metodelor de completare a temelor.

7. Rezumând lecția.

Obiectiv: A oferi o evaluare calitativă a activității clasei și a elevilor individuali.